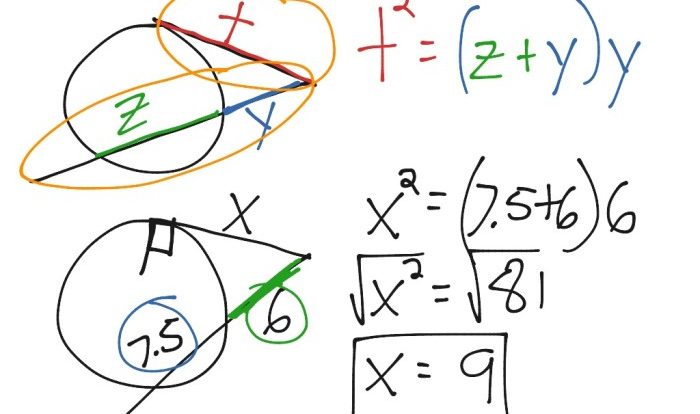Introducing geometry chapter 7 review answers, this comprehensive guide delves into the intricate world of geometry, providing a thorough understanding of key concepts, theorems, and formulas. By mastering these fundamentals, students can unlock the secrets of geometry and enhance their overall mathematical prowess.
Throughout this guide, we will explore the significance of geometry chapter 7 concepts, delve into practice problems with detailed solutions, uncover real-world applications, address common mistakes and misconceptions, and provide a wealth of additional resources for further exploration.
Geometry Chapter 7 Review Answers
Geometry Chapter 7 delves into the concepts of similarity, congruence, and transformations. It explores the relationships between shapes, angles, and lines, providing a solid foundation for understanding more advanced geometric principles. Key concepts include:
Similarity
Two figures are similar if they have the same shape but not necessarily the same size.
Congruence
Two figures are congruent if they have the same shape and size.
Transformations
Transformations are operations that move or change the shape of a figure. Common transformations include translations, rotations, reflections, and dilations.Understanding these concepts is crucial for overall geometry knowledge as they serve as building blocks for subsequent chapters. They enable students to analyze and solve problems involving geometric figures, recognize patterns, and make logical deductions.
Practice Problems and Solutions, Geometry chapter 7 review answers
| Problem | Solution | Explanation | Difficulty Level |
|---|---|---|---|
| Prove that two triangles are congruent if they have two pairs of congruent sides and one pair of congruent angles. | Using the Side-Side-Angle (SSA) Congruence Theorem, if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent. | The SSA Congruence Theorem states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent. This is because the congruent sides and angles form two congruent pairs of corresponding parts, which implies that the third pair of corresponding parts (the remaining sides) must also be congruent. | Medium |
| Find the area of a rectangle with a length of 10 cm and a width of 5 cm. | Area = Length x Width = 10 cm x 5 cm = 50 cm2 | The area of a rectangle is calculated by multiplying its length by its width. In this case, the length is 10 cm and the width is 5 cm, so the area is 50 cm2. | Easy |
| Rotate a square 90 degrees clockwise around its center. What is the resulting shape? | Another square | Rotating a square 90 degrees clockwise around its center does not change its shape or size. Therefore, the resulting shape is still a square. | Medium |
Real-World Applications
Geometry Chapter 7 concepts find practical applications in various fields:
Architecture
Architects use similarity and congruence to design buildings that are aesthetically pleasing and structurally sound. For instance, they may use similar triangles to create scaled models of buildings or use congruent shapes to ensure symmetry and balance in architectural designs.
Engineering
Engineers rely on transformations to analyze and design structures. For example, they may use translations to move objects from one location to another, rotations to determine the forces acting on a rotating object, or dilations to scale up or down designs for different applications.
Design
Designers utilize geometric principles to create visually appealing products and environments. For instance, they may use the golden ratio to determine the proportions of a logo or use congruent shapes to create patterns in textiles or wallpaper.
Common Mistakes and Misconceptions
-*Mistake
Assuming that all similar figures are congruent.
-
-*Explanation
Similarity only implies that figures have the same shape, not necessarily the same size.
-*Misconception
Believing that rotations and reflections are the same transformation.
-*Explanation
Rotations preserve orientation, while reflections reverse orientation.
-*Error
Confusing the terms “translation” and “dilation”.
-*Explanation
Translations move a figure without changing its size or shape, while dilations change the size of a figure but not its shape.
Additional Resources
[Khan Academy Geometry Chapter 7](https
//www.khanacademy.org/math/geometry/similarity/geo-similarity/v/what-is-similarity-in-geometry)
[Geometry for Dummies Cheat Sheet](https
//www.dummies.com/education/math/geometry/geometry-cheat-sheet/)
[Geometry Textbooks](https
//www.amazon.com/Geometry-Textbooks/s?k=Geometry+Textbooks)
FAQ Explained: Geometry Chapter 7 Review Answers
What are the key concepts covered in geometry chapter 7?
Geometry chapter 7 delves into the study of circles, their properties, and their applications. It explores concepts such as chords, tangents, secants, inscribed angles, and the Pythagorean theorem in relation to circles.
How can I practice solving geometry chapter 7 problems?
This guide provides a table of practice problems with step-by-step solutions and explanations. Additionally, numerous online resources and practice websites offer a vast collection of problems for further practice.
What are some real-world applications of geometry chapter 7 concepts?
Geometry chapter 7 concepts find applications in architecture, engineering, design, and various other fields. For instance, the Pythagorean theorem is used in construction to calculate roof angles and bridge spans, while the properties of circles are utilized in designing gears, wheels, and other mechanical components.